主定理（Master Theorem）

主定理的本质，就是看一个递归函数的复杂度是由前半部分子问题规模主导，还是后半部分每一层的递归代价主导。

对于一个递归式，

\[T(n) = aT(n/b) + f(n)\]

前半部分 \(aT(n/b)\) 描述了递归子问题的规模。后半部分 \(f(n)\) 代表了每一层递归的代价。随着递归的深入，函数的总体复杂度是整个递归树每一层复杂度的总和。根据复杂度计算的渐进原则，一些次要的复杂度会被修剪掉。

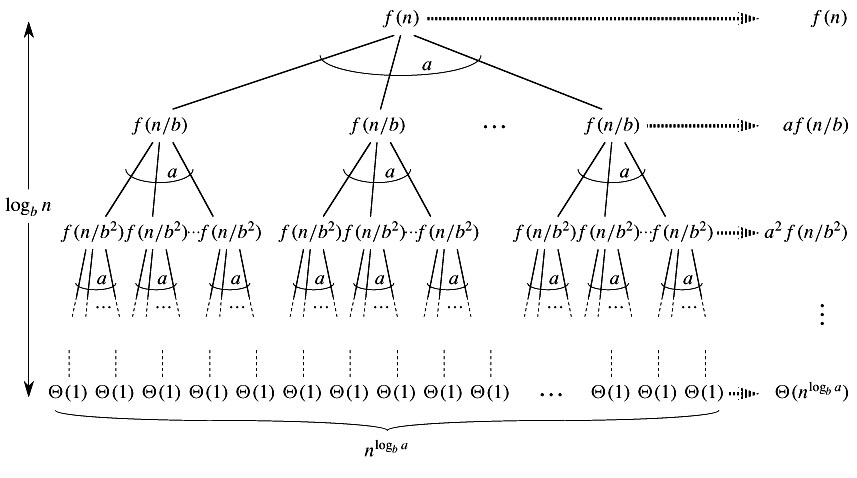
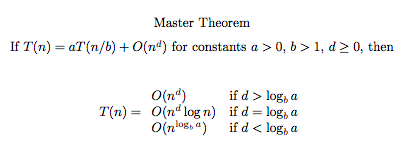
具体分为以下三种情况，

1. \(T(n) = 9T(n/3) + n\) 适用于主定理 case 1：

   前半部分 \(n^{\log_{3}{9}} = n^2\) ，多项式意义地大于后半部分 \(n^1\) 。所以 \(T(n)\) 的复杂度由前半部分\(n^2\)主导。

2. \(T(n) = T(2n/3) + 1\) 适用于主定理 case 2：

   前半部分 \(n^{\log_{3/2}{1}} = n^0 = 1\) ， 和后半部分1同阶。所以 \(T(n)\) 的复杂度等于每层的规模1 乘以递归深度 \(\lg{n}\) ，等于 \(\lg{n}\) 。

3. \(T(n) = 3T(n/4) + n\lg{n}\) 适用于主定理 case 3：

   后半部分 \(n^1\lg{n}\) 多项式意义地大于前半部分 \(n^{\log_{4}{3}}\) 。所以 \(T(n)\) 的复杂度由后半部分 \(n\lg{n}\) 主导。

例外情况

但有些情况会掉进case 2和case 3的缝隙里，

\(T(n) = 2T(n/2) + n\lg{n}\) 适用于主定理 case 2 的一个推广：

前半部分 \(n^{\log_{2}{2}}\) 与后半部分 \(n^1\lg{n}\) 同阶。所以 \(T(n)\) 的复杂度等于每层的规模 \(n\lg{n}\) 乘以递归深度 \(\lg{n}\) ，等于 \(n\lg^{2}{n}\) 。

至于为什么 \(n\lg{n}\) 不是多项式地大于 \(n\) ，是因为多项式意义上的大于是指像下面这种情况，

\[n^{0.2} \times n^{0.8} = n^{0.2+0.8} = n^{1}\]

所以，我们可以说 \(n^{1}\) 是多项式意义上大于 \(n^{0.8}\) 。

但换成 \(\lg{n}\) 就不行，对数 \(\lg{n}\) 在数量级上比 \(n^{0.2}\) 低了一阶，所以 \(\lg{n}\) 渐进小于 \(n^{0.2}\) 。

\[n\lg{n} \div n = \lg{n}\]